Rayleigh model: Difference between revisions
No edit summary |
No edit summary |
||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Rayleigh distillation model describes the evolution of a multiple-phase system in which one phase is continuously removed to the other phase through fractional distillation. Despite its simplicity, it is a powerful framework to describe in particular the isotopic enrichment or depletion as material moves between reservoirs in an equilibrium process. | The Rayleigh distillation model describes the evolution of a multiple-phase system in which one phase is continuously removed to the other phase through fractional distillation. Despite its simplicity, it is a powerful framework to describe in particular the isotopic enrichment or depletion as material moves between reservoirs in an equilibrium fractionation process. | ||
== Model description == | == Model description == | ||
The system applying the Rayleigh equation is | The system applying the Rayleigh equation is often an open system, from which the newly formed phase is immediately removed. For example, the evaporation of natural water bodies, and the formation of precipitation that immediately leaves the system, can be regarded as examples for open systems. However, with some modifications, Rayleigh models can be also applied to other systems. One such system is a closed system (or two-phase equilibrium model; Gat, (1996)), where the material removed from one reservoir accumulates in a second reservoir in such a manner that isotopic equilibrium is maintained between the two reservoirs. An example for this would be the condensation of vapour to droplets in a cloud, without formation and removal of precipitation. | ||
The isotopic enrichment or depletion by the Rayleigh process for both open and closed systems can be mathematically | The isotopic enrichment or depletion by the Rayleigh process for both open and closed systems can be mathematically obtained by different approaches (Fig. 1). The Rayleigh equations that are used to describe the isotopic evolution of the remaining reservoir under different conditions are summarized in Table 1. The isotope ratio of the accumulated removal can be derived using mass conservation of rare isotopes remaining in the reservoir, and the removed component: | ||
<math> fR_\text{remain} + (1-f)R_\text{remove,acc} = R_0 </math>. | |||
In the case of condensation involving both liquid and solid phases, the accumulation is a combination of the removed mass fraction of both phases. First, following the equation above, the total liquid removal is calculated as | |||
<math> R_\text{l,acc} = (R_0-fR_v)/(1-f) </math>. | |||
Then, we consider a separated Rayleigh process by only taking into account of the ongoing formation of the solid phase. Following the same reasoning as above, the isotope ratio of the accumulated solid removal is calculated by | |||
<math> f_iR_\text{i,v} + (1-f_i)R_\text{i,acc} = R_\text{v0} </math>, | |||
where <math>R_\text{v0}</math> and <math>R_\text{i,v}</math> are the isotope ratio of the remaining vapour at the start and the calculating point of the solid condensation stage, respectively, and <math>f_i</math> the fraction of remaining vapour within the solid condensation stage. Finally and again, using mass conservation of the rare isotopes, we obtain the isotope ratio of the total accumulation of the removal by <math> (1-ff_i)R_\text{acc} = (1-f)R_\text{l,acc} + f(1-f_i)R_\text{i,acc} </math>. Corresponding examples of the calculated isotopic evolution profiles are shown in Fig. 2. | |||
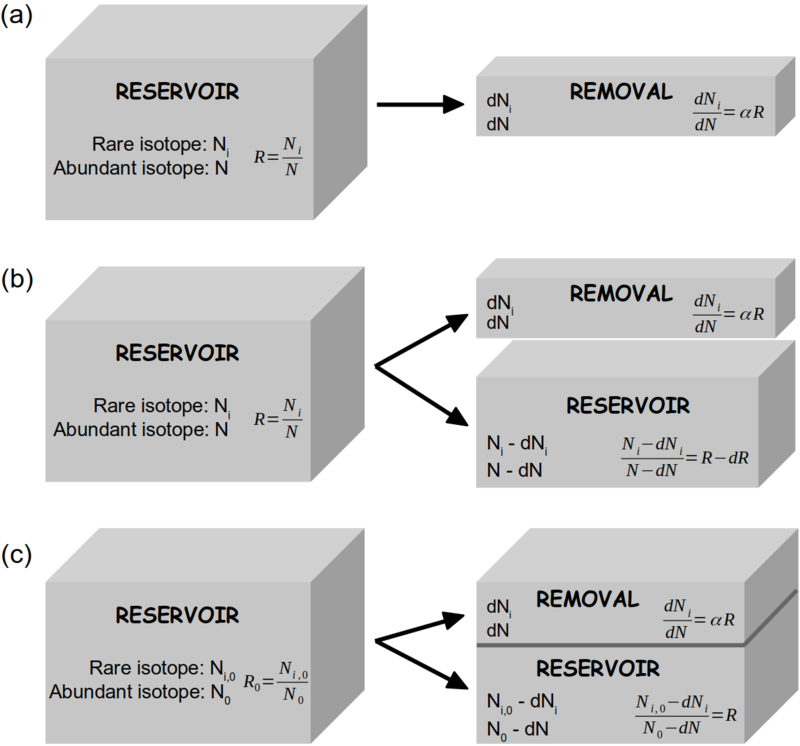
[[File:Rayleigh_model_box_sketch_v2.png|thumb|800px|'''''Figure 1''''' Schematic presentation of the mathematical approaches of the Rayleigh model in open system '''(a, b)''' and closed system '''(c)'''. Adapted from Gat ''et al'' (2001). '''(a)''' From a reservoir containing ''N'' abundant isotopologues (e.g. H<sub>2</sub><sup>16</sup>O) and ''N<sub>i</sub>'' rare isotopologues (e.g. H<sub>2</sub><sup>18</sup>O or HD<sup>16</sup>O) small amounts of both species, ''dN'' and ''dN<sub>i</sub>'' respectively, are being removed under equilibrium fractionation conditions: <math> dN_i/dN = αR </math>. | |||
'''(b)''' The changing isotopic composition of the reservoir is calculated from a mass balance consideration for the rare isotopologues: <math> RN = (R-dR)(N-dN) + αRdN </math>. | |||
'''(c)''' In closed system, the changing isotopic composition of the reservoir can be calculated from a mass balance consideration for the rare isotopologues: <math> R_0N_0 = R(N_0-dN) + αRdN </math>, with the remaining fraction <math> f = (N_0-dN)/N_0 </math>.]] | |||
[[File:Rayleigh_model_plot_v2_CG.png|thumb|800px|'''''Figure 2''''' Isotopic change during '''(a), (c)''' Rayleigh evaporation, and '''(b), (d)''' Rayleigh condensation. Rayleigh evaporation occurs here at 20 °C (thus a constant fractionation factor) for initial liquid compositions of δ<sup>18</sup>O = -10 ‰ and δD = -70 ‰ (''d'' = 10 ‰), in open system with unsaturated (RH = 75 %; black) or saturated (grey) environment, and closed system (blue). In addition, the result of C--G evaporation model (i.e. open system including feedback from a "free atmosphere" which has fixed isotope compositions of δ<sup>18</sup>O = -13 ‰ and δD = -94 ‰ (''d'' = 10 ‰) and a fixed relative humidity (RH = 75 %)) is also presented (red). Rayleigh condensation occurs here under continuous cooling (thus also a contentiously changing fractionation factor) from T = 20 °C and RH = 75 %. The initial vapour compositions are δ<sup>18</sup>O = -13 ‰ and δD = -94 ‰ (''d'' = 10 ‰). For the condensation to ice below 0 °C, two cases are presented. The saturation case (grey) is a classical Rayleigh process where ice crystals from from vapour under equilibrium conditions, using the saturation pressure over ice (''e<sub>i</sub>''). The supersaturation case (black) takes into account the supersaturation over ice, where the ambient vapour pressure is ''e<sub>v</sub> = S<sub>i</sub>*e<sub>i</sub>''. ''S<sub>i</sub>'' is the defined saturation ratio, as ''e<sub>v</sub>/e<sub>i</sub>'', and here takes the form ''S<sub>i</sub> = 1-0.004T'' after Risi ''et al'' (2010a). In this case, the fractionation factor combining equilibrium and kinetic effects given by Jouzel & Merlivat (1984) is used. The equations used in this figure can be found in Table 1.]] | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ ''Table 1'' Rayleigh equations to | |+ ''Table 1'' Rayleigh equations to calculate isotopic evolution of the remaining reservoir under different conditions. The transport resistance is here assumed to be purely due to diffusion (i.e. <math>\rho \propto D^{-1} </math>). | ||
|- | |- | ||
! scope="col"| | ! scope="col"| | ||
| Line 21: | Line 39: | ||
| <math> R = R_0f^{α-1} </math> | | <math> R = R_0f^{α-1} </math> | ||
| <math> δ = (1+δ_0)f^{α-1}-1 </math> | | <math> δ = (1+δ_0)f^{α-1}-1 </math> | ||
| <math> α = \ | | <math> α = \alpha_{vl}<1 </math> | ||
|- | |- | ||
| open system undersaturated | | open system undersaturated | ||
| <math> R = R_0f^{α-1} </math> | | <math> R = R_0f^{α-1} </math> | ||
| <math> δ = (1+δ_0)f^{α-1}-1 </math> | | <math> δ = (1+δ_0)f^{α-1}-1 </math> | ||
| <math> \alpha = \frac{1}{\alpha_k \ | | <math> \alpha = \frac{1}{\alpha_k \alpha_{lv}} </math>, where <math> \alpha_{lv}>1 </math>, and <math> \alpha_k = \frac{D}{D'}(1-h)+h > 1 </math>, with <math> h = \frac{e_v}{e_l} </math> | ||
|- | |- | ||
| closed system | | closed system | ||
| <math> R = \frac{R_0}{f+\alpha(1-f)} </math> | | <math> R = \frac{R_0}{f+\alpha(1-f)} </math> | ||
| <math> \delta = \frac{\delta_0 | | <math> \delta = \frac{1+\delta_0}{f+\alpha(1-f)}-1 </math> | ||
| <math> α = \ | | <math> α = \alpha_{vl}<1 </math> | ||
|- | |- | ||
| C--G model | | C--G model | ||
| Line 42: | Line 60: | ||
| <math> R = R_0f^{α-1} </math> | | <math> R = R_0f^{α-1} </math> | ||
| <math> δ = (1+δ_0)f^{α-1}-1 </math> | | <math> δ = (1+δ_0)f^{α-1}-1 </math> | ||
| <math> α = \ | | <math> α = \alpha_{sv}>1 </math> | ||
|- | |- | ||
| supersaturation over ice | | supersaturation over ice | ||
| <math> R = R_0f^{α-1} </math> | | <math> R = R_0f^{α-1} </math> | ||
| <math> δ = (1+δ_0)f^{α-1}-1 </math> | | <math> δ = (1+δ_0)f^{α-1}-1 </math> | ||
| <math> \alpha = \alpha_k \ | | <math> \alpha = \alpha_k \alpha_{sv} </math>, where <math> \alpha_{sv}>1 </math>, and <math> \alpha_k = \frac{S_i}{\alpha_s \frac{D}{D'}(S_i-1)+1} < 1 </math>, with <math> S_i = \frac{e_v}{e_i} </math> | ||
|- | |- | ||
|} | |} | ||
---- | |||
== Model codes in MATLAB == | == Model codes in MATLAB == | ||
Latest revision as of 20:26, 26 January 2021
The Rayleigh distillation model describes the evolution of a multiple-phase system in which one phase is continuously removed to the other phase through fractional distillation. Despite its simplicity, it is a powerful framework to describe in particular the isotopic enrichment or depletion as material moves between reservoirs in an equilibrium fractionation process.
Model description
The system applying the Rayleigh equation is often an open system, from which the newly formed phase is immediately removed. For example, the evaporation of natural water bodies, and the formation of precipitation that immediately leaves the system, can be regarded as examples for open systems. However, with some modifications, Rayleigh models can be also applied to other systems. One such system is a closed system (or two-phase equilibrium model; Gat, (1996)), where the material removed from one reservoir accumulates in a second reservoir in such a manner that isotopic equilibrium is maintained between the two reservoirs. An example for this would be the condensation of vapour to droplets in a cloud, without formation and removal of precipitation.
The isotopic enrichment or depletion by the Rayleigh process for both open and closed systems can be mathematically obtained by different approaches (Fig. 1). The Rayleigh equations that are used to describe the isotopic evolution of the remaining reservoir under different conditions are summarized in Table 1. The isotope ratio of the accumulated removal can be derived using mass conservation of rare isotopes remaining in the reservoir, and the removed component:
[math]\displaystyle{ fR_\text{remain} + (1-f)R_\text{remove,acc} = R_0 }[/math].
In the case of condensation involving both liquid and solid phases, the accumulation is a combination of the removed mass fraction of both phases. First, following the equation above, the total liquid removal is calculated as
[math]\displaystyle{ R_\text{l,acc} = (R_0-fR_v)/(1-f) }[/math].
Then, we consider a separated Rayleigh process by only taking into account of the ongoing formation of the solid phase. Following the same reasoning as above, the isotope ratio of the accumulated solid removal is calculated by
[math]\displaystyle{ f_iR_\text{i,v} + (1-f_i)R_\text{i,acc} = R_\text{v0} }[/math],
where [math]\displaystyle{ R_\text{v0} }[/math] and [math]\displaystyle{ R_\text{i,v} }[/math] are the isotope ratio of the remaining vapour at the start and the calculating point of the solid condensation stage, respectively, and [math]\displaystyle{ f_i }[/math] the fraction of remaining vapour within the solid condensation stage. Finally and again, using mass conservation of the rare isotopes, we obtain the isotope ratio of the total accumulation of the removal by [math]\displaystyle{ (1-ff_i)R_\text{acc} = (1-f)R_\text{l,acc} + f(1-f_i)R_\text{i,acc} }[/math]. Corresponding examples of the calculated isotopic evolution profiles are shown in Fig. 2.
Figure 1 Schematic presentation of the mathematical approaches of the Rayleigh model in open system (a, b) and closed system (c). Adapted from Gat et al (2001). (a) From a reservoir containing N abundant isotopologues (e.g. H216O) and Ni rare isotopologues (e.g. H218O or HD16O) small amounts of both species, dN and dNi respectively, are being removed under equilibrium fractionation conditions: [math]\displaystyle{ dN_i/dN = αR }[/math]. (b) The changing isotopic composition of the reservoir is calculated from a mass balance consideration for the rare isotopologues: [math]\displaystyle{ RN = (R-dR)(N-dN) + αRdN }[/math]. (c) In closed system, the changing isotopic composition of the reservoir can be calculated from a mass balance consideration for the rare isotopologues: [math]\displaystyle{ R_0N_0 = R(N_0-dN) + αRdN }[/math], with the remaining fraction [math]\displaystyle{ f = (N_0-dN)/N_0 }[/math].
Figure 2 Isotopic change during (a), (c) Rayleigh evaporation, and (b), (d) Rayleigh condensation. Rayleigh evaporation occurs here at 20 °C (thus a constant fractionation factor) for initial liquid compositions of δ18O = -10 ‰ and δD = -70 ‰ (d = 10 ‰), in open system with unsaturated (RH = 75 %; black) or saturated (grey) environment, and closed system (blue). In addition, the result of C--G evaporation model (i.e. open system including feedback from a "free atmosphere" which has fixed isotope compositions of δ18O = -13 ‰ and δD = -94 ‰ (d = 10 ‰) and a fixed relative humidity (RH = 75 %)) is also presented (red). Rayleigh condensation occurs here under continuous cooling (thus also a contentiously changing fractionation factor) from T = 20 °C and RH = 75 %. The initial vapour compositions are δ18O = -13 ‰ and δD = -94 ‰ (d = 10 ‰). For the condensation to ice below 0 °C, two cases are presented. The saturation case (grey) is a classical Rayleigh process where ice crystals from from vapour under equilibrium conditions, using the saturation pressure over ice (ei). The supersaturation case (black) takes into account the supersaturation over ice, where the ambient vapour pressure is ev = Si*ei. Si is the defined saturation ratio, as ev/ei, and here takes the form Si = 1-0.004T after Risi et al (2010a). In this case, the fractionation factor combining equilibrium and kinetic effects given by Jouzel & Merlivat (1984) is used. The equations used in this figure can be found in Table 1.
| Conditions | Equation (R and δ notation) | Fractionation factor used | ||
|---|---|---|---|---|
| Evaporation | open system saturated | [math]\displaystyle{ R = R_0f^{α-1} }[/math] | [math]\displaystyle{ δ = (1+δ_0)f^{α-1}-1 }[/math] | [math]\displaystyle{ α = \alpha_{vl}\lt 1 }[/math] |
| open system undersaturated | [math]\displaystyle{ R = R_0f^{α-1} }[/math] | [math]\displaystyle{ δ = (1+δ_0)f^{α-1}-1 }[/math] | [math]\displaystyle{ \alpha = \frac{1}{\alpha_k \alpha_{lv}} }[/math], where [math]\displaystyle{ \alpha_{lv}\gt 1 }[/math], and [math]\displaystyle{ \alpha_k = \frac{D}{D'}(1-h)+h \gt 1 }[/math], with [math]\displaystyle{ h = \frac{e_v}{e_l} }[/math] | |
| closed system | [math]\displaystyle{ R = \frac{R_0}{f+\alpha(1-f)} }[/math] | [math]\displaystyle{ \delta = \frac{1+\delta_0}{f+\alpha(1-f)}-1 }[/math] | [math]\displaystyle{ α = \alpha_{vl}\lt 1 }[/math] | |
| C--G model | [math]\displaystyle{ R = R_0f^{\alpha-1} }[/math] | [math]\displaystyle{ \delta = (1+\delta_0)f^{\alpha-1}-1 }[/math] | [math]\displaystyle{ \alpha = \frac{\alpha_{vl}-h\frac{R_a}{R_l}}{(1-h)\frac{D}{D'}} }[/math], where [math]\displaystyle{ \alpha_{vl} \lt 1 }[/math] | |
| Condensation | saturation over ice | [math]\displaystyle{ R = R_0f^{α-1} }[/math] | [math]\displaystyle{ δ = (1+δ_0)f^{α-1}-1 }[/math] | [math]\displaystyle{ α = \alpha_{sv}\gt 1 }[/math] |
| supersaturation over ice | [math]\displaystyle{ R = R_0f^{α-1} }[/math] | [math]\displaystyle{ δ = (1+δ_0)f^{α-1}-1 }[/math] | [math]\displaystyle{ \alpha = \alpha_k \alpha_{sv} }[/math], where [math]\displaystyle{ \alpha_{sv}\gt 1 }[/math], and [math]\displaystyle{ \alpha_k = \frac{S_i}{\alpha_s \frac{D}{D'}(S_i-1)+1} \lt 1 }[/math], with [math]\displaystyle{ S_i = \frac{e_v}{e_i} }[/math] | |
Model codes in MATLAB
Rayleigh evaporation
% rayleigh_evaporation.m
%--------------------------------
% Description:
% simple Rayleigh evaporation model, after Stern and Blisniuk, 2002
%--------------------------------
% input variables: T0 (Kelvin), d18O0 (permil), d2H0 (permil);
% system: closed system = 0, open system = 1, C--G model = 2;
% optional: relative humidity (default = 1), d18Oa (permil), d2Ha (permil)
% run example: rayleigh_evaporation(20+273.15,-10,-70,1,0.75)
% rayleigh_evaporation(20+273.15,-10,-70,1)
% rayleigh_evaporation(20+273.15,-10,-70,2)
%--------------------------------
% HS, Do 12 Dez 2013 15:43:28 CET
% YW, structured and included the case of kinetic effect
% and the case of C--G model, 29 Aug 2020
%--------------------------------
function data = rayleigh_evaporation(T0,d18O0,d2H0,system,h,d18Oa,d2Ha)
% %% dubugging
% T0 = 20+273.15;
% d18O0 = -10; % close to Bergen precipitation average
% d2H0 = -70;
% system = 1;
% h = 0.75;
%% fractionation factors
%--------------------------------
% Majoube, M., 1971a: Fractionnement en oxyg`ene-18 entre la glace et la vapeur d’eau. J.
% Chim. Phys., 68, 625–636.
% Majoube, M., 1971b: Fractionnement en oxyg`ene 18 et deut ́erium entre l’eau et sa vapeur. J. Chim.
% Phys., 68, 1423–1436.
% Merlivat, L. and G. Nief, 1967: Fractionnement isotopique lors des changements d‘ ́etat
% solide-vapeur et liquide-vapeur de l’eau `a des temp ́eratures inf ́erieures a ` 0 ◦ C. Tellus,
% 19, 122–127.
%--------------------------------
function d = a2H(T) % T in K
d = 1/exp(24.844e3/(T^2)-76.248/T+52.612e-3); % Majoube 1971b, R_vapour/R_liquid < 1
end
function d = a18O(T) % T in K
d = 1/exp(1137/(T^2)-0.4156/T-0.0020667); % Majoube 1971b, R_vapour/R_liquid < 1
end
%% initialization
% isotope ratios of VSMOW reference water
R2std = 155.76e-6;
R18std = 2005.20e-6;
% initial isotope ratio
R18O0 = (d18O0/1000+1)*R18std;
R2H0 = (d2H0/1000+1)*R2std;
% relative humidity
if ~exist('h','var')
h = 1;
end
% isotope composition of "free atmosphere"
% if not existing, default it to the equilibrium vapour of global average precipitation
if ~exist('d18Oa','var')
d18Oa = -13;
end
if ~exist('d2Ha','var')
d2Ha = -94;
end
R18Oa = (d18Oa/1000+1)*R18std;
R2Ha = (d2Ha/1000+1)*R2std;
% % ouput variables
% data.T = [];
% data.f = [];
% data.d18Ov = [];
% data.d18Ol = [];
% data.d2Hv = [];
% data.d2Hl = [];
% data.dxsv = [];
% data.dxsl = [];
% data.d18Ov_acc = [];
% data.d2Hv_acc = [];
% data.dxsv_acc = [];
%% Rayleigh evaporation process: (0) in closed system (material maintained under two-phase equilibrium)
% i.e., the material removed stays in the closed system and stays in equilibrium with the reservoir
if system == 0
fprintf('Rayleigh evaporation process: in an closed system (material maintained under two-phase equilibrium) \n');
fprintf('T0 = %6.2f K (%4.2f °C) \n', T0, T0-273.15);
fprintf(' f d18Ol d18Ov d2Hl d2Hv dxsl dxsv d18Ov_acc dxsv_acc \n');
i = 1; % iteration steps
for f = 1:-0.02:0 % remaining liquid fraction
% isotope ratio of remaining liquid
R18Ol = R18O0/(a18O(T0) - f*(a18O(T0)-1)); % Gat1996
R2Hl = R2H0/(a2H(T0) - f*(a2H(T0)-1)); % Gat1996
% (1) delta value of remaining liquid
d18Ol = (R18Ol/R18std-1)*1000;
d2Hl = (R2Hl/R2std-1)*1000;
dxsl = d2Hl-8*d18Ol;
% (2) delta value of the instantaneously removed vapour (in equilibrium with the current remaining liquid)
d18Ov = ((d18Ol/1000+1)*a18O(T0)-1)*1000;
d2Hv = ((d2Hl/1000+1)*a2H(T0)-1)*1000;
dxsv = d2Hv-8*d18Ov;
% (3) delta value of the accumulated removed vapour
d18Ov_acc = d18Ov;
d2Hv_acc = d2Hv;
dxsv_acc = dxsv;
fprintf('%8.4f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f\n',f,d18Ol,d18Ov,d2Hl,d2Hv,dxsl,dxsv,d18Ov_acc,dxsv_acc);
% assign to output
data.T(i) = T0;
data.f(i) = f;
data.R18Ol(i) = R18Ol;
data.d18Ol(i) = d18Ol;
data.d18Ov(i) = d18Ov;
data.R2Hl(i) = R2Hl;
data.d2Hl(i) = d2Hl;
data.d2Hv(i) = d2Hv;
data.dxsl(i) = dxsl;
data.dxsv(i) = dxsv;
data.d18Ov_acc(i) = d18Ov_acc;
data.d2Hv_acc(i) = d2Hv_acc;
data.dxsv_acc(i) = dxsv_acc;
% iterate to next step
i = i+1;
end
end
%% Rayleigh evaporation process: (1) in an open system (material is immediately removed)
if system == 1
fprintf('Rayleigh evaporation process: in an open system (material is immediately removed) \n');
fprintf('T0 = %6.2f K (%4.2f °C) \n', T0, T0-273.15);
fprintf(' f d18Ol d18Ov d2Hl d2Hv dxsl dxsv d18Ov_acc dxsv_acc \n');
i = 1; % iteration steps
n = 1; % turbulent exponent in D^n, [0 1], controls the ratio of diffusive transport over turbulent transport of water molecules (Pfahl and Wernli, 2009)
for f = 1:-0.02:0 % remaining liquid fraction
% modified Rayleigh evaporation model including kinectic effct
% during the vapour formation at undersaturated conditions (Jouzel and Merlivat 1984)
% Diffusivities D adopted from Merlivat 1978:
% D_H18O/D_H16O = 0.9723 ± 0.0007
% D_HD16O/D_H216O = 0.9755 ± 0.0009
D18 = 0.9723; % D'/D
D2 = 0.9755; % D'/D
ak_18O = 1/(1/D18^n*(1-h)+h);
ak_2H = 1/(1/D2^n*(1-h)+h);
aeff_18O = a18O(T0) * ak_18O;
aeff_2H = a2H(T0) * ak_2H;
% isotope ratio of remaining liquid
R18Ol = R18O0*f^(aeff_18O-1);
R2Hl = R2H0*f^(aeff_2H-1);
% (1) delta value of remaining liquid
d18Ol = (R18Ol/R18std-1)*1000;
d2Hl = (R2Hl/R2std-1)*1000;
dxsl = d2Hl-8*d18Ol;
% (2) delta value of the instantaneously removed vapour (in equilibrium with the current remaining liquid)
d18Ov = ((d18Ol/1000+1)*aeff_18O-1)*1000;
d2Hv = ((d2Hl/1000+1)*aeff_2H-1)*1000;
dxsv = d2Hv-8*d18Ov;
% (3) isotope ratio of the accumulated removed vapour
R18Ov_acc = R18O0*(1-f^aeff_18O)/(1-f); % Mook 2001, Page 38
R2Hv_acc = R2H0*(1-f^aeff_2H)/(1-f);
% delta value of the accumulated removed vapour
d18Ov_acc = (R18Ov_acc/R18std-1)*1000;
d2Hv_acc = (R2Hv_acc/R2std-1)*1000;
dxsv_acc = d2Hv_acc-8*d18Ov_acc;
% % (3) Calculating the isotope ratio of the accumulated removal using mass conservation approach
% % mass conservation of rare isotopes between the reservoir and formed removal: f*Rl+(1-f)*Rv_acc=R0,
% % after rearranging, we have: Rv_acc=(R0-f*Rl)/(1-f)
% R18Ov_acc2 = (R18O0-f*R18Ol)/(1-f);
% R2Hv_acc2 = (R2H0-f*R2Hl)/(1-f);
% data.d18Ov_acc2(i) = (R18Ov_acc2/R18std-1)*1000;
% data.d2Hv_acc2(i) = (R2Hv_acc2/R2std-1)*1000;
% data.dxsv_acc2(i) = data.d2Hv_acc2(i)-8*data.d18Ov_acc2(i);
fprintf('%8.4f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f\n',f,d18Ol,d18Ov,d2Hl,d2Hv,dxsl,dxsv,d18Ov_acc,dxsv_acc);
% assign to output
data.T(i) = T0;
data.f(i) = f;
data.R18Ol(i) = R18Ol;
data.d18Ol(i) = d18Ol;
data.d18Ov(i) = d18Ov;
data.R2Hl(i) = R2Hl;
data.d2Hl(i) = d2Hl;
data.d2Hv(i) = d2Hv;
data.dxsl(i) = dxsl;
data.dxsv(i) = dxsv;
data.d18Ov_acc(i) = d18Ov_acc;
data.d2Hv_acc(i) = d2Hv_acc;
data.dxsv_acc(i) = dxsv_acc;
% iterate to next step
i = i+1;
end
end
%% Rayleigh evaporation process: (2) in a "free atmosphere" of fixed humidity and isotope composition (C--G model)
if system == 2
fprintf('Rayleigh evaporation process: in an open system (material is immediately removed) \n');
fprintf('T0 = %6.2f K (%4.2f °C) \n', T0, T0-273.15);
fprintf(' f d18Ol d18Ov d2Hl d2Hv dxsl dxsv d18Ov_acc dxsv_acc \n');
% turbulent exponent in D^n, [0 1], controls the ratio of diffusive transport over turbulent transport of water molecules (Pfahl and Wernli, 2009)
% n~0.5 for an open water body under natural conditions, n~0.58 for a falling raindrop (Stewart1975), n~1 for soils and leaves
n = 1;
df = 0.02;
i = 1; % iteration steps
for f = 1:-df:0 % remaining liquid fraction
% modified Rayleigh evaporation model including kinectic effct
% during the vapour formation at undersaturated conditions (Jouzel and Merlivat 1984)
% Diffusivities D adopted from Merlivat 1978:
% D_H18O/D_H16O = 0.9723 ± 0.0007
% D_HD16O/D_H216O = 0.9755 ± 0.0009
D18 = 0.9723; % D'/D
D2 = 0.9755; % D'/D
if i==1
aeff_18O = (a18O(T0) - h*R18Oa/R18O0) / ((1-h)*1/D18^n);
aeff_2H = (a2H(T0) - h*R2Ha/R2H0) / ((1-h)*1/D2^n);
% isotope ratio of remaining liquid
f1 = 1;
R18Ol = R18O0*f1^(aeff_18O-1);
R2Hl = R2H0*f1^(aeff_2H-1);
else
aeff_18O = (a18O(T0) - h*R18Oa/data.R18Ol(i-1)) / ((1-h)*1/D18^n);
aeff_2H = (a2H(T0) - h*R2Ha/data.R2Hl(i-1)) / ((1-h)*1/D2^n);
% isotope ratio of remaining liquid
f1 = 1-df; % fraction remaining relative to previous stage
R18Ol = data.R18Ol(i-1)*f1^(aeff_18O-1);
R2Hl = data.R2Hl(i-1)*f1^(aeff_2H-1);
end
% (1) delta value of remaining liquid
d18Ol = (R18Ol/R18std-1)*1000;
d2Hl = (R2Hl/R2std-1)*1000;
dxsl = d2Hl-8*d18Ol;
% (2) delta value of the instantaneously removed vapour (in equilibrium with the current remaining liquid)
d18Ov = ((d18Ol/1000+1)*aeff_18O-1)*1000;
d2Hv = ((d2Hl/1000+1)*aeff_2H-1)*1000;
dxsv = d2Hv-8*d18Ov;
% % (3) isotope ratio of the accumulated removed vapour
% R18Ov_acc = R18O0*(1-f^aeff_18O)/(1-f); % Mook 2001, Page 38
% R2Hv_acc = R2H0*(1-f^aeff_2H)/(1-f);
% % delta value of the accumulated removed vapour
% d18Ov_acc = (R18Ov_acc/R18std-1)*1000;
% d2Hv_acc = (R2Hv_acc/R2std-1)*1000;
% dxsv_acc = d2Hv_acc-8*d18Ov_acc;
% (3) Calculating the isotope ratio of the accumulated removal using mass conservation approach
% mass conservation of rare isotopes between the reservoir and formed removal: f*Rl+(1-f)*Rv_acc=R0,
% after rearranging, we have: Rv_acc=(R0-f*Rl)/(1-f)
R18Ov_acc = (R18O0-f*R18Ol)/(1-f);
R2Hv_acc = (R2H0-f*R2Hl)/(1-f);
% delta value of the accumulated removed vapour
d18Ov_acc = (R18Ov_acc/R18std-1)*1000;
d2Hv_acc = (R2Hv_acc/R2std-1)*1000;
dxsv_acc = d2Hv_acc-8*d18Ov_acc;
fprintf('%8.4f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f\n',f,d18Ol,d18Ov,d2Hl,d2Hv,dxsl,dxsv,d18Ov_acc,dxsv_acc);
% assign to output
data.T(i) = T0;
data.f(i) = f;
data.R18Ol(i) = R18Ol;
data.d18Ol(i) = d18Ol;
data.d18Ov(i) = d18Ov;
data.R2Hl(i) = R2Hl;
data.d2Hl(i) = d2Hl;
data.d2Hv(i) = d2Hv;
data.dxsl(i) = dxsl;
data.dxsv(i) = dxsv;
data.d18Ov_acc(i) = d18Ov_acc;
data.d2Hv_acc(i) = d2Hv_acc;
data.dxsv_acc(i) = dxsv_acc;
% iterate to next step
i = i+1;
end
end
end
% fin
Rayleigh condensation
% rayleigh_condensation.m
%--------------------------------
% Description:
% - simple Rayleigh condensation model, after Stern and Blisniuk, 2002
% - temperature dependent fractionation factor varies at each step during cooling process
% (1) isobaric cooling: e.g., air parcel advects to cold regions
% (2) or pseudoadiabatic cooling: e.g., updraft or lift of surface air parcel
% - therefore, the isotope ratio is calculated as: R(n+1) = R(n)(q(n+1)/q(n))^(a-1)
%--------------------------------
% input variables: T0 (Kelvin), RH0 (%), d18O0 (permil), d2H0 (permil),
% sice: saturation conditions over ice when temperature <0 degree
% > 1: using the constant supersaturation given as sice;
% = 1: meaning alpha_k = 1, thus no supersaturation;
% = 0: using formula Si = 1-0.004*T (in Celsius)
% run example: rayleigh_condensation(20+273.15,0.75,-13,-94,0)
% rayleigh_condensation(20+273.15,0.75,-13,-94,1)
% rayleigh_condensation(20+273.15,0.75,-13,-94,1.2)
%--------------------------------
% HS, Do 12 Dez 2013 15:43:28 CET
% YW, structured and included kinetic effect, 29 Aug 2020
%--------------------------------
% YW, 26 Mar 2020
% limitation:
% Rayleigh condensation model only reflects the process of water vapor removing
% and ignores: mixing of air masses, cloud water-vapor isotope exchange,
% subcloud droplet evaporation, and radiative cooling or heating.
%--------------------------------
function data = rayleigh_condensation(T0,RH0,d18O0,d2H0,sice)
% %% for debugging
% T0 = 20+273.15;
% RH0 = 0.75; % Craig-Gordon, 1965 (Fig. 15)
% d18O0 = -13;
% d2H0 = -94;
% sice = 0;
% RH0 = 0.91; % 20161207 AR event at Bergen
% d18O0 = -12.5;
% d2H0 = -100;
%% functions adopted
% fractionation factors
%--------------------------------
% Majoube, M., 1971a: Fractionnement en oxyg`ene-18 entre la glace et la vapeur d’eau. J.
% Chim. Phys., 68, 625–636.
% Majoube, M., 1971b: Fractionnement en oxyg`ene 18 et deut ́erium entre l’eau et sa vapeur. J. Chim.
% Phys., 68, 1423–1436.
% Merlivat, L. and G. Nief, 1967: Fractionnement isotopique lors des changements d‘ ́etat
% solide-vapeur et liquide-vapeur de l’eau `a des temp ́eratures inf ́erieures a ` 0 °C. Tellus,
% 19, 122–127.
%--------------------------------
function d = a2H(T) % T in Kelvin
if T >= 273.15 % above 0 celsius
d = exp(24.844e3/(T^2)-76.248/T+52.612e-3); % Majoube 1971b, R_liquid/R_vapour > 1
else
d = exp(16289./T.^2 - 0.0945); % Merlivat & Nief 1967, R_solid/R_vapour > 1
end
end
function d = a18O(T) % T in Kelvin
if T >= 273.15 % above 0 celsius
d = exp(1137/(T^2)-0.4156/T-0.0020667); % Majoube 1971b, R_liquid/R_vapour > 1
else
d = exp(11.839./T - 0.028224); % Majoube 1971a, R_solid/R_vapour > 1
end
end
% supersaturation with respect to ice
% Si = 1 − λT, with λ = 0.004. From Graf 2017 dissertation, page 53, Fig 3.1
% (as in Risi et al., 2010b, after Jouzel and Merlivat 1984.)
% Risi, C., S. Bony, F. Vimeux, and J. Jouzel, 2010b: Water-stable isotopes in the LMDZ4
% general circulation model: Model evaluation for present-day and past climates and
% applications to climatic interpretations of tropical isotopic records.
% sice: > 1: using the constant supersaturation given here;
% = 1: meaning alpha_k = 1, thus no supersaturation;
% = 0: using formula Si = 1-0.004*T (in Celsius)
function s = si(T)
if sice >= 1
s = sice;
else % elseif sice == 0
s = 1-0.004*(T-273.15);
end
end
% vapour saturation pressure
function es = esat(T) % T in Kelvin
if T >= 273.15
% es = 611*exp((17.27*T)/(273+T)); % T in celsius
es = 611*exp(17.27*(T-273.15)/T); % T in Kelvin
else
% Saturation vapour pressure over ice (Murphy and Koop, 2005) for T > 110 K:
es_ice = exp(9.550426 - 5723.265/T + 3.53068*log(T) - 0.00728332*T);
% the actual saturation vapour pressure
es = es_ice * si(T);
end
end
% saturated vapour mixing ratio
function ws = wsat(es,p)
ws = 0.622*es/(p-es);
end
% pressure at height of z
function p = pressure(z)
p0 = 101325; % Pa
z0 = 8000; % m scale height
p = p0*exp(-z/z0);
end
% moist adiabatic lapse rate [Curry and Webster,1999] (cited after Stern and Blisniuk, 2002)
function lr = gamma(ws,T) % T in Kelvin
% physical constants
g = 9.80665; % m/s^2 the gravitational acceleration
Cpd = 1.00464e3; % J/kg/K the specific heat capacity of dry air at constant pressure
L = 2.5104e6; % J/kg the latent heat of vaporization or sublimation
Rd = 287.04; % J/kg/K the specific gas constant for dry air
lr = g/Cpd*(1+L*ws/Rd/T)/(1+0.622*L*L*ws/Rd/Cpd/T/T); % [°C/m]
end
%% initialization
% isotope ratios of VSMOW reference water
R2std = 155.76e-6;
R18std = 2005.20e-6;
% initial isotope ratio
R18O0 = (d18O0/1000+1)*R18std;
R2H0 = (d2H0/1000+1)*R2std;
dxs0 = R2H0-8*R18O0;
% initial conditions
f = 1.0; % remaining vapour fractionation
z = 0.0; % elevation
p = pressure(z);
w0 = RH0*wsat(esat(T0),p); % kg/kg
% convert water mixing ratio unit
md = 28.97; % [g/mol] dry air molar mass
mv = 18.02; % [g/mol] water vapour molar mass
wconc0 = w0*md/mv*1e6; % [kg/kg] --> [ppmv]
rh = RH0;
dt = 0.5; % temperature step
T = T0+dt;
%% for the circumstance of isobaric cooling
%% (1) cool to saturation
fprintf('Rayleigh condensation process: in an open system (material is immediately removed) \n');
fprintf('T0 = %6.2f K (%4.2f °C) \n', T0, T0-273.15);
fprintf(' T (°C) d18Ov d2Hv dxsv rh f WConc[ppmv] \n');
n = 1; % iteration number
while rh < 0.99
T = T-dt; % decrease temperature by dt °C at each iteration
ws = wsat(esat(T),p); % saturated water mixing ratio at each iteration
rh = w0/ws; % RH at each iteration
wconc = wconc0; % [kg/kg] --> [ppmv]
fprintf('%8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f \n',T-273.15,d18O0,d2H0,dxs0,rh,f,wconc);
% assign to output
data.T(n) = T;
data.f(n) = f;
data.rh(n) = rh;
data.Wconc(n) = wconc;
data.R18O(n) = R18O0;
data.R2H(n) = R2H0;
data.d18O(n) = d18O0;
data.dD(n) = d2H0;
data.dxs(n) = d2H0-8*d18O0;
data.d18Oc(n) = NaN; % condensate
data.d2Hc(n) = NaN;
data.dxsc(n) = NaN;
data.d18O_acc(n) = NaN; % accumulated condensate (liquid+solid)
data.d2H_acc(n) = NaN;
data.dxs_acc(n) = NaN;
% iterate to next step
n = n+1;
end
fprintf('Reached saturation now\n');
ws0 = w0;
%% (2) continue to cool and form liquid condensate
while T > 273.15 % isobaric cooling with condensation to 0 °C
T = T-dt; % decrease temperature by dt °C at each iteration
ws = wsat(esat(T),p); % saturated water mixing ratio at each iteration
wconc = ws*md/mv*1e6; % [kg/kg] --> [ppmv]
f = ws/ws0;
if n == 1
f1 = ws/ws0;
% isotope ratio of remaining vapour
R18Ov = R18O0*f1^(a18O(T)-1); % R(n) = R(n-1)(q(n)/q(n-1))^(a-1)
R2Hv = R2H0*f1^(a2H(T)-1);
else
f1 = wconc/data.Wconc(n-1); % q(n)/q(n-1)
% isotope ratio of remaining vapour
R18Ov = data.R18O(n-1)*f1^(a18O(T)-1); % R(n) = R(n-1)(q(n)/q(n-1))^(a-1)
R2Hv = data.R2H(n-1)*f1^(a2H(T)-1);
end
% (1) delta value of remaining vapour
d18Ov = (R18Ov/R18std-1)*1000;
d2Hv = (R2Hv/R2std-1)*1000;
dxsv = d2Hv - 8*d18Ov;
% (2) delta value of the instantaneously removed condensate (in equilibrium with the current remaining vapour)
d18Oc = ((d18Ov/1000+1)*a18O(T)-1)*1000;
d2Hc = ((d2Hv/1000+1)*a2H(T)-1)*1000;
dxsc = d2Hc-8*d18Oc;
% (3) Calculating the isotope ratio of the accumulated removal using mass conservation approach
% mass conservation of rare isotopes between the reservoir and formed removal: f*Rv + (1-f)*Rl_acc = R0,
% after rearranging, we have: Rl_acc = (R0-f*Rv)/(1-f)
R18Ol_acc = (R18O0-f*R18Ov)/(1-f);
R2Hl_acc = (R2H0-f*R2Hv)/(1-f);
d18Ol_acc = (R18Ol_acc/R18std-1)*1000;
d2Hl_acc = (R2Hl_acc/R2std-1)*1000;
dxsl_acc = d2Hl_acc-8*d18Ol_acc;
fprintf('%8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f \n',T-273.15,d18Ov,d2Hv,dxsv,rh,f,wconc);
% assign to output
data.T(n) = T;
data.f(n) = f;
data.rh(n) = rh;
data.Wconc(n) = wconc;
data.R18O(n) = R18Ov;
data.R2H(n) = R2Hv;
data.d18O(n) = d18Ov;
data.dD(n) = d2Hv;
data.dxs(n) = dxsv;
data.rh(n) = rh;
data.d18Oc(n) = d18Oc;
data.d2Hc(n) = d2Hc;
data.dxsc(n) = dxsc;
data.d18O_acc(n) = d18Ol_acc;
data.d2H_acc(n) = d2Hl_acc;
data.dxs_acc(n) = dxsl_acc;
% iterate to next step
n = n+1;
end
fprintf('Have cooled to 0 celcius now \n');
ws0_ice = ws;
R18O0 = R18Ov;
R2H0 = R2Hv;
f0 = f;
%% (3) continue to cool and form solid condensate
% considering mixed-phase cloud: subsaturated over liquid droplets and supersaturated over ice crystals
% closure assumption: liquid droplets --> evaporate to vapour --> deposite on ice crystals
% therefore: when T<0 celsius, the reduced fraction of vapour is due to its deposit on ice crystals with a fractionation
% factor alpha_eff = alpha_eq*alpha_k taking into account the kinetic effct under the supersaturation condition.
% i.e.: we start a new Rayleigh condensation model starting with the remaining vapour
% after the liquid condensation stage above, and use the new factionation factor alpha_eff
while T > -60+273.15
T = T-dt;
ws = wsat(esat(T),p);
wconc = ws*md/mv*1e6; % [kg/kg] --> [ppmv]
f = ws/ws0; % the total fraction of remaining vapour through all stages
fi = ws/ws0_ice; % the fraction of remaing vapour in the ice condensation stage only
% modified Rayleigh condensation model including kinectic effct
% during the ice formation at supersaturated conditions (Jouzel and Merlivat 1984)
% Diffusivities D adopted from Merlivat 1978:
% D_H18O/D_H16O = 0.9723 ± 0.0007
% D_HD16O/D_H216O = 0.9755 ± 0.0009
ak_18O = si(T)/(a18O(T)*1/0.9723*(si(T)-1) + 1);
ak_2H = si(T)/(a2H(T)*1/0.9755*(si(T)-1) + 1);
aeff_18O = a18O(T) * ak_18O;
aeff_2H = a2H(T) * ak_2H;
if n == 1
f1 = ws/ws0;
% isotope ratio of remaining vapour
R18Ov = R18O0*f1^(aeff_18O-1); % R(n) = R(n-1)(q(n)/q(n-1))^(a-1)
R2Hv = R2H0*f1^(aeff_2H-1);
else
f1 = wconc/data.Wconc(n-1); % q(n)/q(n-1)
% isotope ratio of remaining vapour
R18Ov = data.R18O(n-1)*f1^(aeff_18O-1); % R(n) = R(n-1)(q(n)/q(n-1))^(a-1), and Jouzel and Merlivat, 1984
R2Hv = data.R2H(n-1)*f1^(aeff_2H-1);
end
% (1) delta value of remaining vapour
d18Ov = (R18Ov/R18std-1)*1000;
d2Hv = (R2Hv/R2std-1)*1000;
dxsv = d2Hv - 8*d18Ov;
% (2) delta value of the instantaneously removed condensate (in equilibrium with the current remaining vapour)
d18Oc = ((d18Ov/1000+1)*aeff_18O-1)*1000;
d2Hc = ((d2Hv/1000+1)*aeff_2H-1)*1000;
dxsc = d2Hc-8*d18Oc;
% (3) Calculating the isotope ratio of the accumulated removal using mass conservation approach
% (i) mass conservation of rare isotopes between the reservoir and formed removal:
% fi*Rv + (1-fi)*Ri_acc = Rv0,
% where fi is the fraction of remaining vapour in the ice condensation stage, and
% Rv0 is the isotope ratio of the remaining vapour after liquid condensation stage
% after rearranging, we have: Ri_acc = (Rv0-fi*Rv)/(1-fi)
R18Oi_acc = (R18O0-fi*R18Ov)/(1-fi);
R2Hi_acc = (R2H0-fi*R2H0)/(1-fi);
% d18Oi_acc = (R18Oi_acc/R18std-1)*1000;
% d2Hi_acc = (R2Hi_acc/R2std-1)*1000;
% dxsi_acc = d2Hi_acc-8*d18Oi_acc;
% (ii) the total accumulation is sum of the liquid (1-f0) and solid condensate (f0*(1-fi))
% (1-f0*fi)*R_acc = (1-f0)*Rl_acc + (f0*(1-fi))*Ri_acc
R18O_acc = ((1-f0)*R18Ol_acc + (f0*(1-fi))*R18Oi_acc)/(1-f0*fi);
R2H_acc = ((1-f0)*R2Hl_acc + (f0*(1-fi))*R2Hi_acc)/(1-f0*fi);
d18O_acc = (R18O_acc/R18std-1)*1000;
d2H_acc = (R2H_acc/R2std-1)*1000;
dxs_acc = d2H_acc-8*d18O_acc;
fprintf('%8.2f %8.2f %8.2f %8.2f %8.2f %8.2f %8.2f \n',T-273.15,d18Ov,d2Hv,dxsv,rh,f,wconc);
% assign to output
data.T(n) = T;
data.f(n) = f;
data.rh(n) = rh;
data.Wconc(n) = wconc;
data.R18O(n) = R18Ov;
data.R2H(n) = R2Hv;
data.d18O(n) = d18Ov;
data.dD(n) = d2Hv;
data.dxs(n) = dxsv;
data.rh(n) = rh;
data.d18Oc(n) = d18Oc;
data.d2Hc(n) = d2Hc;
data.dxsc(n) = dxsc;
data.d18O_acc(n) = d18O_acc;
data.d2H_acc(n) = d2H_acc;
data.dxs_acc(n) = dxs_acc;
% iterate to next step
n = n+1;
end
%% for the circumstance of pseudoadiabatic cooling
% - establish the relationship between T and z
z = 0;
p = pressure(z);
n = 1;
for T = T0:-dt:-60+273.15
data.T(n) = T;
data.z(n) = z;
data.p(n) = p;
% the elevation change
ws = wsat(esat(T),p);
lr = gamma(ws,T); % lapse rate
dz = dt/lr; % dt = lr*dz
% the new elevation and pressure
z = z+dz;
p = pressure(z);
data.lr(n) = lr;
% iterate to next step
n = n+1;
end
end
% fin
Example of usage
1. Generate the desired data sets
%% create data sets % Rayleigh evaporation T0 = 20+273.15; d18O0 = -10; % close to Bergen precipitation average d2H0 = -70; h = 0.75; % relative humidity de_ok = rayleigh_evaporation(T0,d18O0,d2H0,1,h); % in an open system, unsaturated (including kinetic effect) de_oe = rayleigh_evaporation(T0,d18O0,d2H0,1); % in an open system, saturated (equilibrium) de_cl = rayleigh_evaporation(T0,d18O0,d2H0,0); % in a closed system de_CG = rayleigh_evaporation(T0,d18O0,d2H0,2,h); % C--G model % Rayleigh condensation T0 = 20+273.15; RH0 = 0.75; % Craig-Gordon, 1965 (Fig. 15) d18O0 = -13; d2H0 = -94; % > 1: using the constant supersaturation given as sice; % = 1: % = 0: dc_ln = rayleigh_condensation(T0,RH0,d18O0,d2H0,0); % using linear formula Si = 1-0.004*T (in Celsius) dc_no = rayleigh_condensation(T0,RH0,d18O0,d2H0,1); % meaning alpha_k = 1, thus no supersaturation, e = e_ice dc_11 = rayleigh_condensation(T0,RH0,d18O0,d2H0,1.1); % using the constant supersaturation as given
2. Plot Rayleigh evaporation and condensation profiles.
As an example, Fig. 2 is created using the data sets generated from the above step and using the plotting codes from below.
%% plot Rayleigh evaporation and condensation model
fs = 14;
clear h
figure
set(gcf,'color','white','position',[0 0 1200 1150],'PaperPositionMode','auto');
% left_color = [0 0 0]; % black
% right_color = [0 0.4470 0.7410]; % blueish % blue [0 0 1];
% set(gcf,'defaultAxesColorOrder',[left_color; right_color]);
% Rayleigh evaporation
h(1) = subplot(2,2,1);
% set(h(1),'Position', [0.1 0.56 0.38 0.38]);
hold on
pe(1) = plot(de_ok.f,de_ok.d18Ol,'k-','linewidth',2);
pe(2) = plot(de_ok.f,de_ok.d18Ov,'k--','linewidth',2);
pe(3) = plot(de_ok.f,de_ok.d18Ov_acc,'k:','linewidth',2);
pe(4) = plot(de_oe.f,de_oe.d18Ol,'-','color',[0.6 0.6 0.6],'linewidth',2); %'color',[0.3010 0.7450 0.9330],
pe(5) = plot(de_oe.f,de_oe.d18Ov,'--','color',[0.6 0.6 0.6],'linewidth',2);
pe(6) = plot(de_oe.f,de_oe.d18Ov_acc,':','color',[0.6 0.6 0.6],'linewidth',2);
pe(7) = plot(de_cl.f,de_cl.d18Ol,'-','color',[0.3010 0.7450 0.9330],'linewidth',2);
pe(8) = plot(de_cl.f,de_cl.d18Ov,'--','color',[0.3010 0.7450 0.9330],'linewidth',2);
pe(9) = plot(de_cl.f,de_cl.d18Ov_acc,':','color',[0.3010 0.7450 0.9330],'linewidth',2);
pe(10) = plot(de_CG.f,de_CG.d18Ol,'-','color',[0.8500 0.3250 0.0980],'linewidth',2);
pe(11) = plot(de_CG.f,de_CG.d18Ov,'--','color',[0.8500 0.3250 0.0980],'linewidth',2);
pe(12) = plot(de_CG.f,de_CG.d18Ov_acc,':','color',[0.8500 0.3250 0.0980],'linewidth',2);
ylim(h(1),[-30 40]);
xlabel('Residual water fraction','fontsize',fs);
ylabel(['\delta^{18}O / ',char(8240)],'fontsize',fs);
lgd1 = legend(h(1),pe(1:3),'residual water','instant vapour','total vapour removed','Location','northwest');
lgd1_pos = lgd1.Position;
lgd1.FontSize = fs;
% lgd1.Visible = 'off';
% 2nd axes
a2 = axes('position',get(h(1),'position'),'visible','off'); % create the same axes but set it invisible
% lgd2 = legend(a2,pe(4:6),'residual water','instant vapour','total vapour removed','Location','northwest');
% lgd2.FontSize = fs;
lgd2 = legend(a2,pe(4:6),'','','','location','northwest','box','off');
lgd2_pos = lgd1_pos+[-lgd1_pos(3)*0.304 -lgd1_pos(4)*0.58 0 lgd1_pos(4)*0.5]; % move the 2nd legend to the desired position
set(lgd2,'box','off','Position',lgd2_pos);
% 3rd axes
a3 = axes('position',get(gca,'position'),'visible','off'); % create the same axes but set it invisible
lgd3 = legend(a3,pe(7:9),'','','','location','northwest','box','off');
lgd3_pos = lgd1_pos+[-lgd1_pos(3)*0.304 -lgd1_pos(4)*0.79 0 lgd1_pos(4)*0.5]; % move the 2nd legend to the desired position
set(lgd3,'box','off','Position',lgd3_pos);
% % 4th axes
a4 = axes('position',get(gca,'position'),'visible','off'); % create the same axes but set it invisible
lgd4 = legend(a4,pe(10:12),'','','','location','northwest','box','off');
lgd4_pos = lgd1_pos+[-lgd1_pos(3)*0.304 -lgd1_pos(4)*0.88 0 lgd1_pos(4)*0.5]; % move the 2nd legend to the desired position
set(lgd4,'box','off','Position',lgd4_pos);
% add text
text(h(1),0.41,8.5,'open','FontSize',fs,'Rotation',30)
text(h(1),0.30,13.2,'(unsaturated)','FontSize',fs,'Rotation',53)
text(h(1),0.60,-3,'open','FontSize',fs,'Rotation',15,'color',[0.6 0.6 0.6])
text(h(1),0.48,-0.5,'(saturated)','FontSize',fs,'Rotation',20,'color',[0.6 0.6 0.6])
text(h(1),0.75,-10,'closed','FontSize',fs,'Rotation',7,'Color',[0.3010 0.7450 0.9330])
text(h(1),0.8,1.5,'C-G model','color',[0.8500 0.3250 0.0980],'FontSize',fs,'Rotation',15)
h(3) = subplot(2,2,3);
% set(h(3),'Position', [0.1 0.1 0.38 0.38]);
hold on
plot(de_ok.f,de_ok.dxsl,'k-','linewidth',2)
plot(de_ok.f,de_ok.dxsv,'k--','linewidth',2)
plot(de_ok.f,de_ok.dxsv_acc,'k:','linewidth',2)
plot(de_oe.f,de_oe.dxsl,'-','color',[0.6 0.6 0.6],'linewidth',2)
plot(de_oe.f,de_oe.dxsv,'--','color',[0.6 0.6 0.6],'linewidth',2)
plot(de_oe.f,de_oe.dxsv_acc,':','color',[0.6 0.6 0.6],'linewidth',2)
plot(de_cl.f,de_cl.dxsl,'-','color',[0.3010 0.7450 0.9330],'linewidth',2)
plot(de_cl.f,de_cl.dxsv,'--','color',[0.3010 0.7450 0.9330],'linewidth',2)
plot(de_cl.f,de_cl.dxsv_acc,':','color',[0.3010 0.7450 0.9330],'linewidth',2)
plot(de_CG.f,de_CG.dxsl,'-','color',[0.8500 0.3250 0.0980],'linewidth',2)
plot(de_CG.f,de_CG.dxsv,'--','color',[0.8500 0.3250 0.0980],'linewidth',2)
plot(de_CG.f,de_CG.dxsv_acc,':','color',[0.8500 0.3250 0.0980],'linewidth',2)
ylim(h(3),[-60 70]);
set(h(3),'ytick',-60:20:65);
xlabel('Residual water fraction','fontsize',fs);
ylabel(['\itd / ',char(8240)],'fontsize',fs);
% Rayleigh condensation
h(4) = subplot(2,2,4);
% set(h(4),'Position', [0.56 0.1 0.38 0.38]);
hold on
pc(4) = plot(dc_no.Wconc,dc_no.dxsc,'-','color',[0.6 0.6 0.6],'linewidth',2);
pc(5) = plot(dc_no.Wconc,dc_no.dxs,'--','color',[0.6 0.6 0.6],'linewidth',2);
pc(6) = plot(dc_no.Wconc,dc_no.dxs_acc,':','color',[0.6 0.6 0.6],'linewidth',2);
ylim(gca,[-20 50]);
xlabel('Water mixing ratio / ppmv','fontsize',fs);
set(gca,'XTick',2000:3000:16000);
ylabel(['\itd / ',char(8240)],'fontsize',fs);
% 2nd axis
ax1_pos = get(gca,'position'); % position of first axes
axes('Position',ax1_pos,'XAxisLocation','top','YAxisLocation','right','Color','none','YTickLabel','','FontSize',fs,'TickDir','out');
hold on
pc(1) = plot(dc_ln.f,dc_ln.dxsc,'k-','linewidth',2); % [0.3010 0.7450 0.9330]
pc(2) = plot(dc_ln.f,dc_ln.dxs,'k--','linewidth',2);
pc(3) = plot(dc_ln.f,dc_ln.dxs_acc,'k:','linewidth',2);
% pc(7) = plot(dc_11.f,dc_11.dxsc,'-','color',[0.3010 0.7450 0.9330],'linewidth',2);
% pc(8) = plot(dc_11.f,dc_11.dxs,'--','color',[0.3010 0.7450 0.9330],'linewidth',2);
% pc(9) = plot(dc_11.f,dc_11.dxs_acc,':','color',[0.3010 0.7450 0.9330],'linewidth',2);
ylim(gca,[-20 50]);
xlabel('Residual vapour fraction','fontsize',fs);
% 3rd axis
axes('Position',ax1_pos+[0 0 0 -ax1_pos(4)],'XAxisLocation','top','YColor','w','YTick',[],'Color','none','TickDir','out','FontSize',fs);
hold on
pc(7) = plot(dc_ln.Wconc,20*ones(size(dc_ln.Wconc)),'k-'); % [0.3010 0.7450 0.9330]
ylim(gca,[-20 50]);
xlabel('T / °C','fontsize',fs);
set(gca,'XTick',[dc_ln.Wconc(81) dc_ln.Wconc(61:-10:11)],'XTickLabel',[-20 -10:5:15])
h(2) = subplot(2,2,2);
% set(h(2),'Position', [0.56 0.56 0.38 0.38]);
hold on
pc(4) = plot(dc_no.Wconc,dc_no.d18Oc,'-','color',[0.6 0.6 0.6],'linewidth',2); % [0 0.4470 0.7410]
pc(5) = plot(dc_no.Wconc,dc_no.d18O,'--','color',[0.6 0.6 0.6],'linewidth',2);
pc(6) = plot(dc_no.Wconc,dc_no.d18O_acc,':','color',[0.6 0.6 0.6],'linewidth',2);
ylim(h(2),[-60 -2]);
xlabel('Water mixing ratio / ppmv','fontsize',fs);
set(gca,'XTick',2000:3000:16000);
ylabel(['\delta^{18}O / ',char(8240)],'fontsize',fs);
% 2nd axis
ax1_pos = get(gca,'position'); % position of first axes
axes('Position',ax1_pos,'XAxisLocation','top','YAxisLocation','right','Color','none','YTickLabel','','FontSize',fs,'TickDir','out');
hold on
pc(1) = plot(dc_ln.f,dc_ln.d18Oc,'k-','linewidth',2); % [0.3010 0.7450 0.9330]
pc(2) = plot(dc_ln.f,dc_ln.d18O,'k--','linewidth',2);
pc(3) = plot(dc_ln.f,dc_ln.d18O_acc,'k:','linewidth',2);
% pc(7) = plot(dc_11.f,dc_11.d18Oc,'-','color',[0.3010 0.7450 0.9330],'linewidth',2);
% pc(8) = plot(dc_11.f,dc_11.d18O,'--','color',[0.3010 0.7450 0.9330],'linewidth',2);
% pc(9) = plot(dc_11.f,dc_11.d18O_acc,':','color',[0.3010 0.7450 0.9330],'linewidth',2);
ylim(gca,[-60 -2]);
xlabel('Residual vapour fraction','fontsize',fs);
lg = legend(h(2),pc(1:3),'instant liquid/ice','residual vapour','total liquid/ice removed');
% lg = legend(h(2),pc(4:6),'instant liquid/ice','residual vapour','total liquid/ice removed');
set(lg,'Position',[0.69 0.66 0.20 0.06],'FontSize',fs);
lg_pos = lg.Position;
% 3rd axis
axes('Position',ax1_pos+[0 -ax1_pos(4)*0.2 0 -ax1_pos(4)*0.8],'XAxisLocation','top','YColor','w','YTick',[],'Color','none');
hold on
pc(7) = plot(dc_ln.Wconc,-2+zeros(size(dc_ln.d18Oc)),'k-'); % [0.3010 0.7450 0.9330]
ylim(gca,[-60 -2]);
xlabel('T / °C','fontsize',fs);
set(gca,'XTick',[dc_ln.Wconc(81) dc_ln.Wconc(61:-10:11)],'XTickLabel',[-20 -10:5:15],'FontSize',fs,'TickDir','out');
lg2 = legend(gca,pc(4:6),'','','','location','east','box','off');
lg2_pos = lg_pos+[-lg_pos(3)*0.405 +lg_pos(4)*0.02 0 lg_pos(4)*0.117]; % move the 2nd legend to the desired position
set(lg2,'box','off','Position',lg2_pos);
% add text
text(h(2),1300,-36,'super','FontSize',fs,'Rotation',65)
text(h(2),2150,-27.5,'saturation','FontSize',fs,'Rotation',50)
text(h(2),1200,-25,'saturation','FontSize',fs,'Rotation',50,'Color',0.6*[1 1 1])
set([h(1) h(3)],'XDir','reverse','box','on');
set(h(:),'color','none','FontSize',fs,'tickdir','out'); % ,'YAxisLocation','left','ticklength',[0 0],'ygrid','on','xgrid','on'
annotation('textbox',[0.05 0.96 0.02 0.02],'String','(a)','FitBoxToText','on','FontSize',fs+6,'LineStyle','none');
annotation('textbox',[0.49 0.96 0.02 0.02],'String','(b)','FitBoxToText','on','FontSize',fs+6,'LineStyle','none');
annotation('textbox',[0.05 0.48 0.02 0.02],'String','(c)','FitBoxToText','on','FontSize',fs+6,'LineStyle','none');
annotation('textbox',[0.49 0.48 0.02 0.02],'String','(d)','FitBoxToText','on','FontSize',fs+6,'LineStyle','none');
% print('-depsc','-r300','/scratch/home/figs/thesis/Rayleigh_model_plot');
% print('-dpng','-r300','/scratch/home/figs/thesis/Rayleigh_model_plot');