Rayleigh model

Rayleigh distillation model describes the evolution of a multiple-phases system in which one phase is continuously removed to the other phase through fractional distillation. Despite its simplicity, it is a powerful framework to describe in particular the isotopic enrichment or depletion as material moves between reservoirs in an equilibrium process.

Model description

The system applying the Rayleigh equation is normally an open system from which the formed material is immediately removed. For example, the evaporation of the natural water bodies, and the formation of falling precipitation can be regarded as open systems. However, the Rayleigh equation can be also applied to other systems. One such system is a closed system (or two-phase equilibrium model; Gat, (1996)), where the material removed from one reservoir accumulates in a second reservoir in such a manner that isotopic equilibrium is maintained between the two reservoirs. An example would be the condensation of vapour to droplets in a cloud (with no falling precipitation).

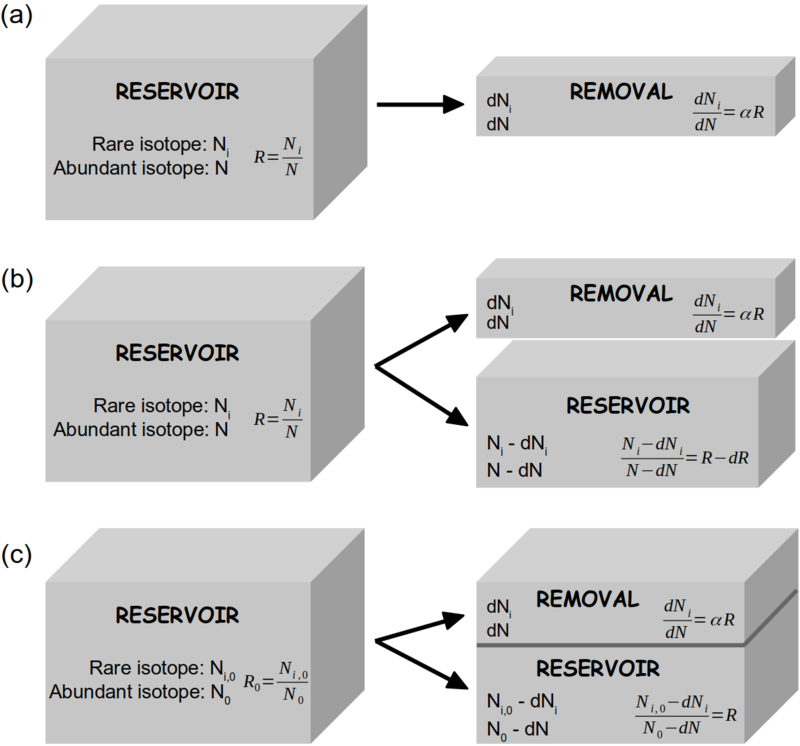
The isotopic enrichment or depletion by the Rayleigh process for both open and closed systems can be mathematically established by different approaches (Fig. 1).

Figure 1 Schematic presentation of the mathematical approaches of the Rayleigh model in open system (a, b) and closed system (c). Adapted from Gat et al (2001). (a) From a reservoir containing N abundant isotopologues (e.g. H_2{16}O) and N_i rare isotopologues (e.g. H_2{18}O or HD{16}O) small amounts of both species, dN and dN_i respectively, are being removed under equilibrium fractionation conditions: dN_i/dN = α*R. (b) The changing isotopic composition of the reservoir is calculated from a mass balance consideration for the rare isotopologues: R*N = (R-dR)*(N-dN) + α*R*dN. (c) In closed system, the changing isotopic composition of the reservoir can be calculated from a mass balance consideration for the rare isotopologues: R_0*N_0 = R*(N_0-dN) + α*R*dN, with the remaining fraction f = (N_0-dN)/N_0.

Item	Quantity	Price
Bread	0.3 kg	$0.65
Butter	0.125 kg	$1.25
Total		$1.90

Model visualization

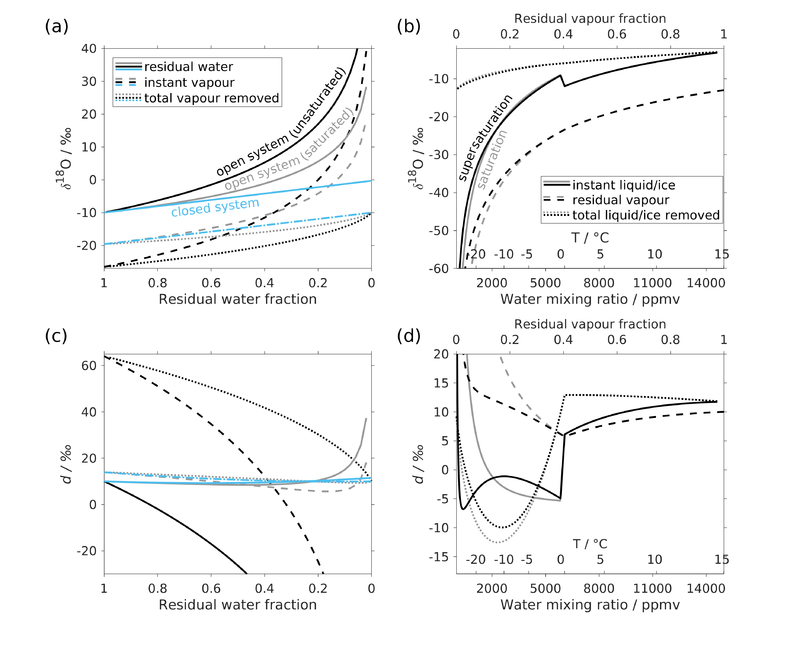
Figure 2 Isotopic change during (a), (c) Rayleigh evaporation, and (b), (d) Rayleigh condensation. Rayleigh evaporation occurs at 20 C (thus a constant fractionation factor) for initial liquid compositions of δ18O = -10 ‰ and δD = -70 ‰ (d = 10 ‰), in open system with unsaturated (RH = 75 %; black) or saturated (grey) environment, and closed system (blue). Rayleigh condensation occurs under continuous cooling (thus also a contentiously changing fractionation factor) from T = 20 C and RH = 75 %. The initial vapour compositions are δ18O = -13 ‰ and δD = -94 ‰ (d = 10 ‰). For the condensation to ice below 0 C, two circumstances are presented. The saturation circumstance (grey) is a classical Rayleigh process where vapour forms ice crystals under equilibrium conditions, using the saturation pressure over ice (e_i). The supersaturation circumstance (black) takes into account the supersaturation over ice where the ambient vapour pressure is e_v = S_i*e_i. S_i is the defined saturation ratio, as e_v/e_i, and here takes the form S_i = 1-0.004*T after Risi et al 2010a. In this circumstance, the fractionation factor combining equilibrium and kinetic effects given by Jouzel & Merlivat (1984) is used.

Example of usage

The mergetime command will create one new output file with a common time axis. Therefore, all inputfiles must have a common time axis, and the same variables, essentially they must have the same netcdf file format.

Here is an example for how to create a monthly file from the daily TPS-3100 (Hotplate) data files: